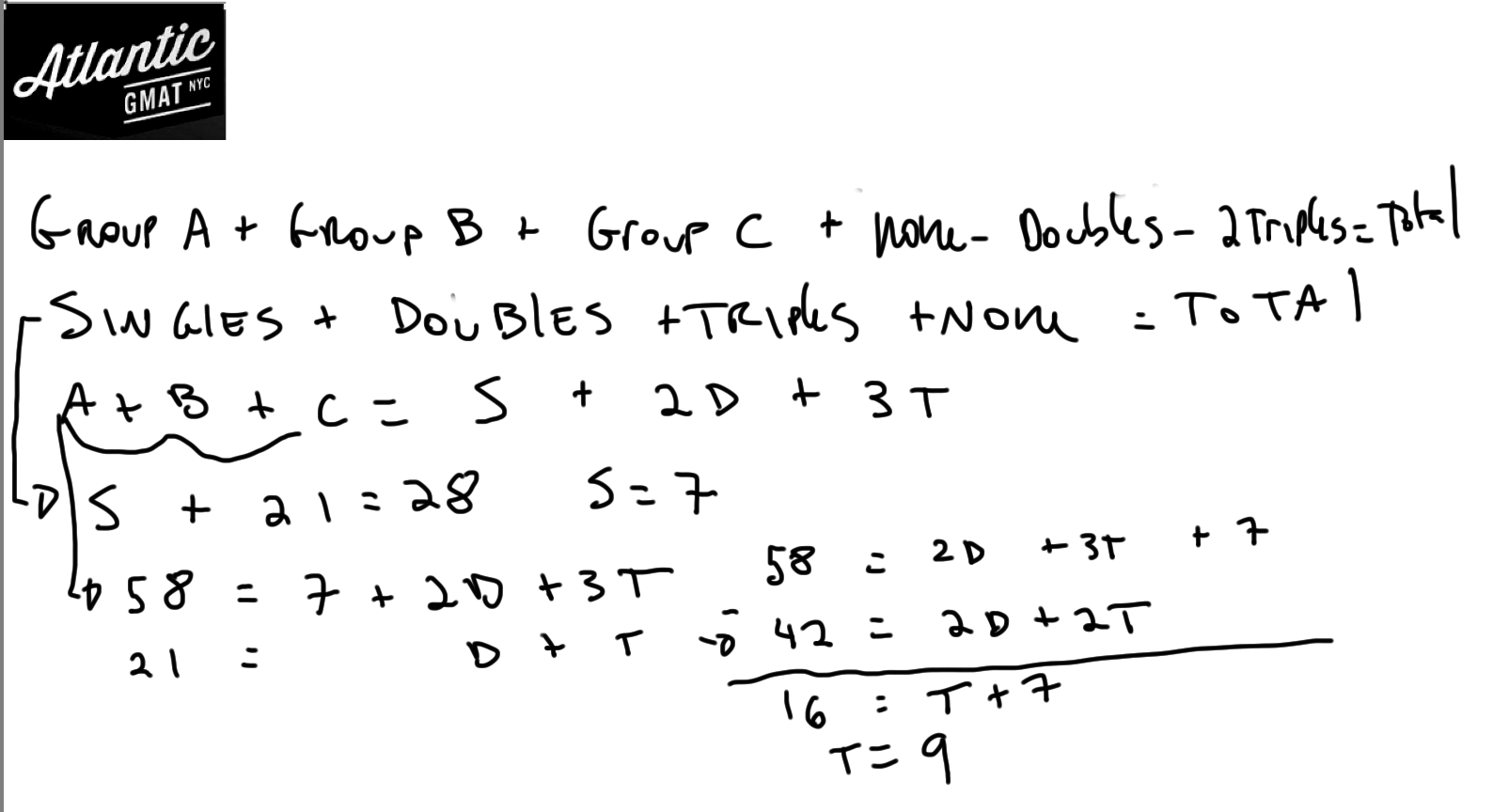Overlapping Sets Formula Gre

Practice problems on overlapping sets with target test prep experts scott woodbury stewart and jeffrey miller in this 40 minute webinar covering basic and advanced concepts tested on the gre.

Overlapping sets formula gre. The n students are divided as below. First let s look at this example. There are two basic 3 set venn diagram formulas that we already know. The box denotes a class having n students.

Like many questions on the gmat the most important part of solving the question is to fully understand and rephrase it. Total group1 group2 both neither in the example above 40 is total 25 is group1 12 is group2 and 8 is both. Overlapping set questions are very common but present a complex set of difficulties. To reiterate the key steps.

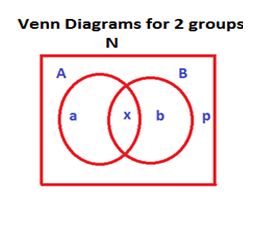
And the overlap formula is. We will discuss below representing data using the method of venn diagrams for 2 groups and 3 groups. Most overlapping sets on the gmat have two distinct groups. Students take french and or spanish or neither pianists play either classical and or jazz or neither people like either qdoba and or baja fresh definitely neither.

For example let s say that in a room of 20 people there are 12 dog owners and 14 cat owners. First from the above figure consider the following data. Most of these are self explanatory but we will look into the details of the less commonly known three set venn formulas. Chipotle please and for these situations the familiar double set matrix approach works best.

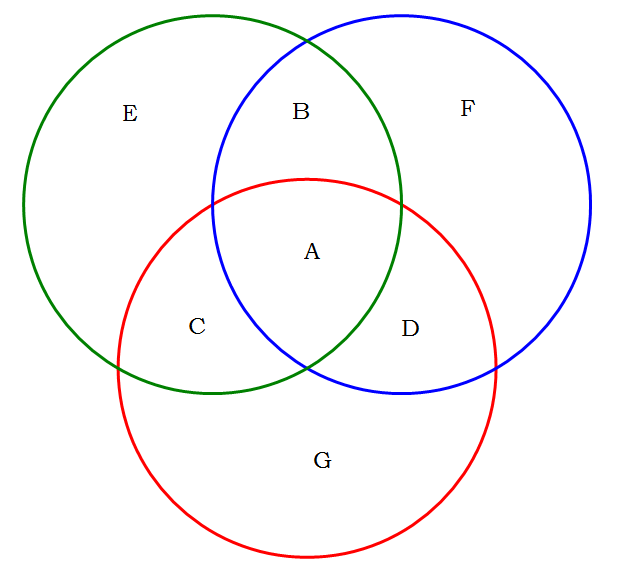
This venn diagram shows overlapping sets that contain letters. The overlapping sets formula. Identify how many decision variables there are. Formula for two overlapping sets a classic gmat setup involves a large group that is subdivided into two potentially overlapping subgroups.

Group1 and group2 are interchangeable basically g1 g2 is the sum of all of the people who do one or the other but that sum double counts the number who do both. However as with two sets we ll write in an easier to remember notation in just a moment. Today we will look at all of the various venn diagram formulas floating around on three overlapping sets.